Um círculo é diferente de um círculo: explicação. Círculo e círculo: exemplos, fotos. A fórmula para o comprimento de um círculo e a área de um círculo: comparação

Vamos entender o que são um círculo e um círculo. A fórmula para a área de um círculo e o comprimento de um círculo.

Todos os dias encontramos muitos objetos que formar um círculo ou vice-versa. Às vezes surge a pergunta, o que é um círculo e como ele difere de um círculo. Claro, todos nós tivemos aulas de geometria, mas às vezes não faz mal atualizar seu conhecimento com explicações bastante simples.

Qual é o comprimento de um círculo e a área de um círculo: definição

Então, um círculo é uma linha curva fechada que limita ou, ao contrário, forma um círculo. Um pré-requisito para um círculo é que ele tenha um centro e todos os pontos sejam equidistantes dele. Simplificando, um círculo é um aro de ginástica (ou como é frequentemente chamado de bambolê) em uma superfície plana.

O comprimento de um círculo é o comprimento total da mesma curva que forma o círculo. Como se sabe, independentemente do tamanho do círculo, a razão entre seu diâmetro e comprimento é igual ao número π = 3,141592653589793238462643.

Segue-se que π=L/D, onde L é o comprimento do círculo e D é o diâmetro do círculo.

Se você conhece o diâmetro, o comprimento pode ser encontrado usando uma fórmula simples: L= π* D

Se o raio for conhecido: L=2 πR

Descobrimos o que é um círculo e podemos prosseguir para a definição de um círculo.

Um círculo é uma figura geométrica que é cercada por um círculo. Ou, um círculo é uma figura cuja borda consiste em um grande número de pontos equidistantes do centro da figura. Toda a área dentro de um círculo, incluindo seu centro, é chamada de círculo.

Vale a pena notar que o raio e o diâmetro do círculo e do círculo dentro dele são os mesmos. E o diâmetro, por sua vez, é duas vezes maior que o raio.

Um círculo tem uma área em um plano, que pode ser encontrada usando uma fórmula simples:

S= πR2

Onde S é a área do círculo, e R é o raio desse círculo.

Como um círculo difere de um círculo: Explicação

A principal diferença entre um círculo e um círculo é que um círculo é uma figura geométrica e um círculo é curva fechada. Observe também as diferenças entre um círculo e um círculo:

• Um círculo é uma linha fechada, e um círculo é a área dentro desse círculo;
• Um círculo é uma linha curva em um plano, e um círculo é um espaço fechado em um anel por um círculo;
• Semelhança entre círculo e círculo: raio e diâmetro;
• Um círculo tem um único centro;
• Se o espaço dentro do círculo estiver sombreado, ele se transforma em um círculo;
• Um círculo tem comprimento, mas um círculo não, e vice-versa, um círculo tem uma área que um círculo não tem.

Círculo e círculo: exemplos, foto

Para maior clareza, sugerimos que você considere a foto, que mostra um círculo à esquerda e círculo à direita.

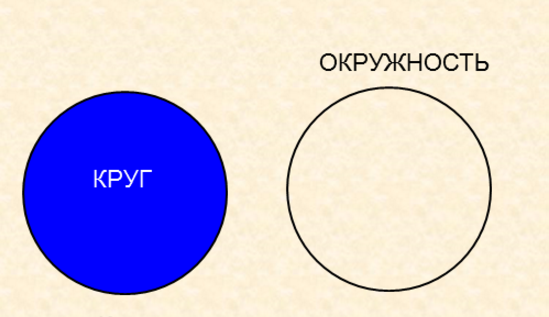
A fórmula para o comprimento de um círculo e a área de ​um círculo: comparação

A fórmula para o comprimento de um círculo L=πR 2

A fórmula para a área de um círculo S= πR2

Observe que o raio e o número π estão presentes em ambas as fórmulas. Recomenda-se aprender essas fórmulas de cor, pois são as mais simples e certamente serão úteis na vida cotidiana e no trabalho.

Área de um círculo pelo comprimento da circunferência: fórmula

A fórmula para a área de um círculo pode ser calculado se apenas uma quantidade for conhecida - o comprimento do círculo que limita o círculo de dados

S=π(L/2π)=L2/4π, onde S é a área do círculo, L é o comprimento do círculo.

Vídeo: O que é um círculo, circunferência e raio