Área de um círculo: fórmula. Por que a área de um círculo descrito e inscrito em um quadrado é igual a um triângulo retângulo isósceles, um trapézio retângulo isósceles?

Como encontrar a área de um círculo? Primeiro encontre o raio. Aprenda a resolver tarefas simples e complexas.

Um círculo é uma curva fechada. Qualquer ponto na linha do círculo será equidistante do ponto central. Um círculo é uma forma plana, portanto, resolver a tarefa de encontrar a área é simples. Neste artigo, consideraremos como encontrar a área de um círculo inscrito em um triângulo, trapézio, quadrado e descrito próximo a essas figuras.

Área de um círculo: fórmula usando raio, diâmetro, comprimento de um círculo, exemplos de resolução de problemas

Para encontrar a área de ​​uma figura, você precisa saber que tal é o raio, o diâmetro e o número π.

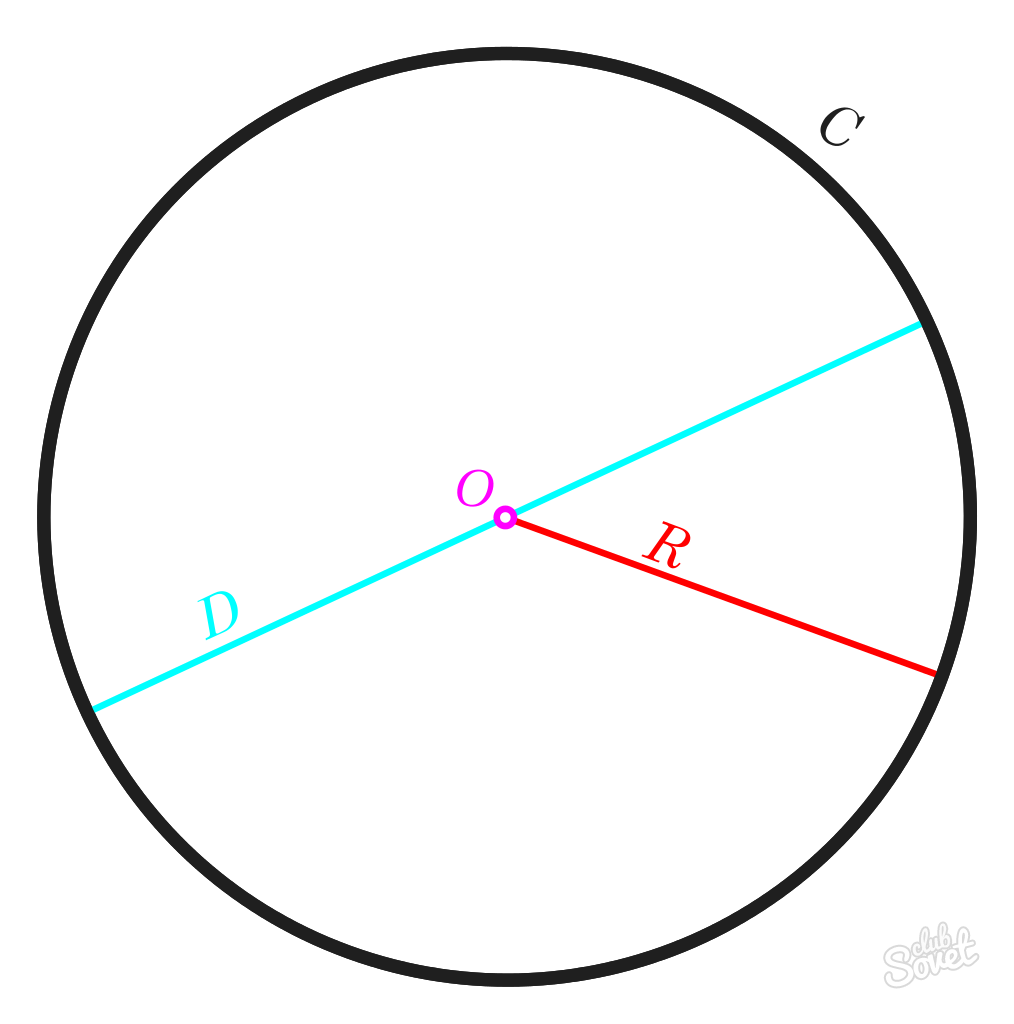
Raio R é a distância limitada pelo centro do círculo. Os comprimentos de todos os raios R de um círculo serão iguais.

Diâmetro D é uma linha entre quaisquer dois pontos em um círculo que passa pelo ponto central. O comprimento deste segmento é igual ao comprimento do raio R multiplicado por 2.

O número π é um valor constante igual a 3,1415926. Em matemática, esse número geralmente é arredondado para 3,14.

A fórmula para encontrar a área de um círculo através do raio:

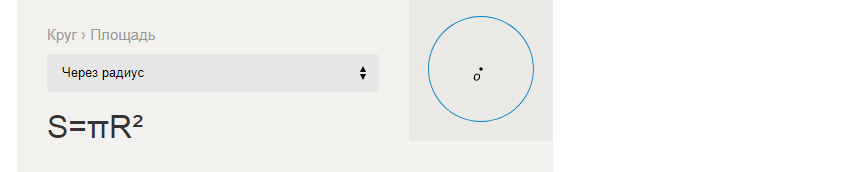
Exemplos de resolução de tarefas para encontrar a área S de um círculo através do raio R:

---------- ---------------------------- --

Tarefa: Encontre a área de um círculo, se seu raio for 7 cm.

Solução: S=πR2, S=3,14*72, S=3,14*49=153,86 cm2.

Resposta: A área de um círculo é 153,86 cm2.

A fórmula para encontrar a área S de um círculo através do diâmetro D:

Exemplos de resolução de tarefas para encontrar S se D for conhecido:

--------- --------------------------------

Quest: Encontre S de um círculo, se seu D for igual a 10 cm.

Solução: P=π*d2/4, P=3,14*102/4=3,14*100/4=314/4=78,5 cm2.

Resposta: A área de uma figura redonda plana é de 78,5 cm2.

Encontrando S de um círculo, se o comprimento do círculo for conhecido:

Primeiro, encontramos o que é o raio. O comprimento do círculo é calculado pela fórmula: L=2πR, portanto, o raio R será igual a L/2π. Agora encontramos a área do círculo usando a fórmula através de R.

Vamos considerar a solução no exemplo do problema:

) ------------ -----------------------------

Tarefa: Encontre a área de um círculo, se o comprimento do círculo L for conhecido — 12 cm.

Solução: Primeiro encontramos o raio: R=L/2π=12/2*3,14=12/6,28=1,91.

Agora encontramos a área através do raio: S=πR2=3,14*1,912=3,14*3,65=11,46 cm2.

Resposta: A área de um círculo é 11,46 cm2.

Área de um círculo inscrito em um quadrado: fórmula, exemplos de resolução de problemas

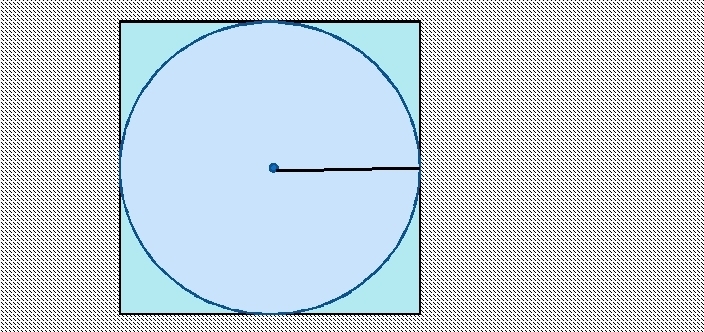
Encontrar a área de um círculo inscrito em um quadrado é simples. O lado do quadrado é o diâmetro do círculo. Para encontrar o raio, você precisa dividir o lado por 2.

A fórmula para encontrar a área de um círculo inscrito em um quadrado:

Exemplos de resolução de problemas para encontrar a área de um círculo inscrito em um quadrado:

-- ---------------------------------- ----

Tarefa No. 1: O lado de uma figura quadrada, que é igual a 6 centímetros, é conhecido. Encontre a área S do círculo inscrito.

Solução: S=π(a/2)2=3,14(6/2)2=3,14*9=28,26 cm2.

Resposta: A área de uma figura redonda plana é 28,26 cm2.

----------------------------------------- -----------

Tarefa #2 :Encontre S de um círculo inscrito em uma figura quadrada e seu raio se um lado for igual a a=4 veja

Resolva da seguinte forma : Primeiro encontramos R=a/2=4/2=2 veja

Agora vamos encontrar a área do círculo S=3,14*22=3,14*4=12,56 cm2.

Resposta: A área de uma figura circular plana é 12,56 cm2.

Área de um círculo circunscrito a um quadrado: fórmula, exemplos de resolução de problemas

É um pouco mais difícil encontrar a área de uma figura redonda descrita em torno de um quadrado. Mas, conhecendo a fórmula, você pode calcular rapidamente esse valor.

Fórmula para encontrar S de um círculo circunscrito a uma figura quadrada:

Exemplos de resolução de problemas para encontrar a área de um círculo descrito em torno de uma figura quadrada:

Problema

Área de um círculo inscrito em um triângulo retângulo e isósceles: fórmula, exemplos de resolução de problemas

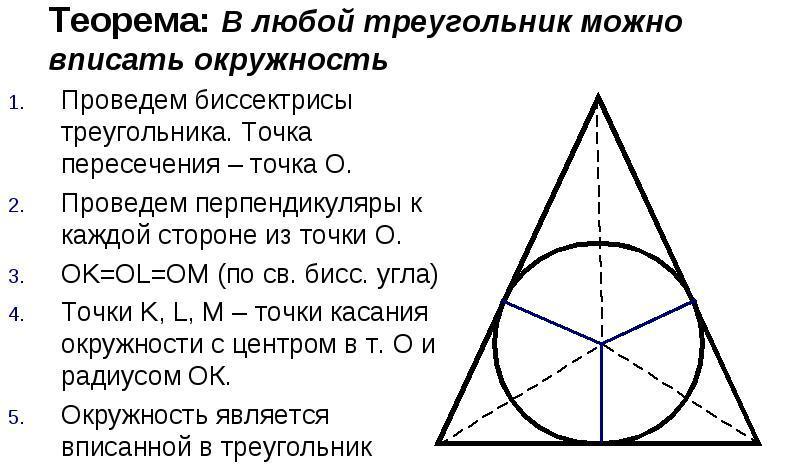
Um círculo inscrito em uma figura triangular é um círculo que toca todos os três lados do triângulo. Qualquer figura triangular pode ser inscrita com um círculo, mas apenas um. O centro do círculo será o ponto de intersecção das bissetrizes do ângulo do triângulo.

Fórmula para encontrar a área de um círculo inscrito em um triângulo isósceles:

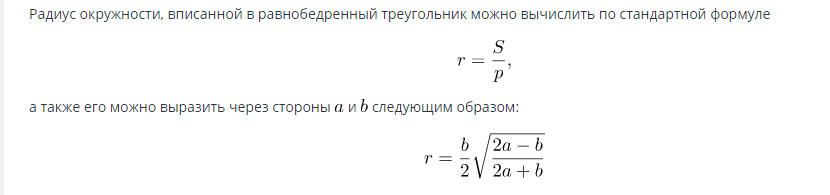
Quando o raio é conhecido, a área pode ser calculada usando a fórmula: S=πR2.

Fórmula para encontrar a área de um círculo inscrito em um triângulo retângulo:

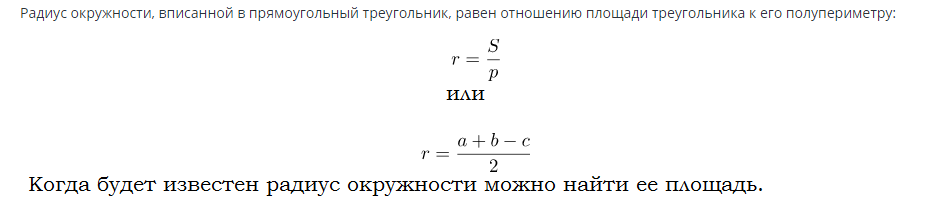
Exemplos de soluções de problemas:

Problema # 1

)

Se neste problema você também precisa encontrar a área de um círculo com um raio de 4 cm, então você pode fazê-lo pela fórmula: S=πR2

Tarefa #2

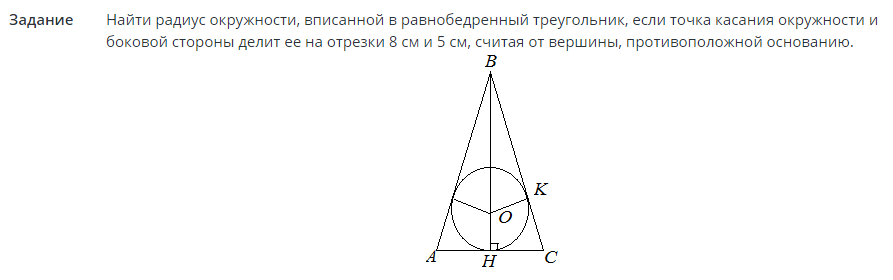
Soluções:

Agora que o raio é conhecido, a área do círculo pode ser encontrada em termos do raio. Veja a fórmula acima no texto.

Tarefa #3

Área de um círculo circunscrito a um triângulo retângulo e isósceles: fórmula, exemplos de resolução de problemas

Todas as fórmulas para encontrar a área de um círculo se resume ao fato de que primeiro você precisa encontrar seu raio. Quando o raio é conhecido, encontrar a área é simples, conforme descrito acima.

​​​​

A área de um círculo circunscrito a um triângulo retângulo e isósceles é encontrada pela seguinte fórmula:

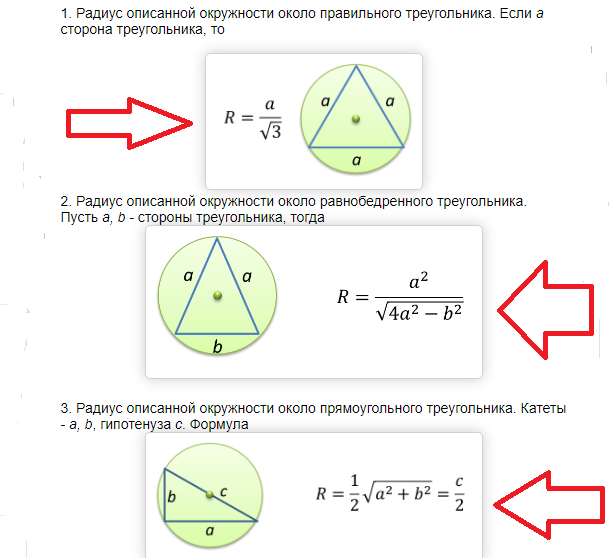
Exemplos de resolução de problemas:

Aqui está outro exemplo de resolução de um problema usando a fórmula de Heron.

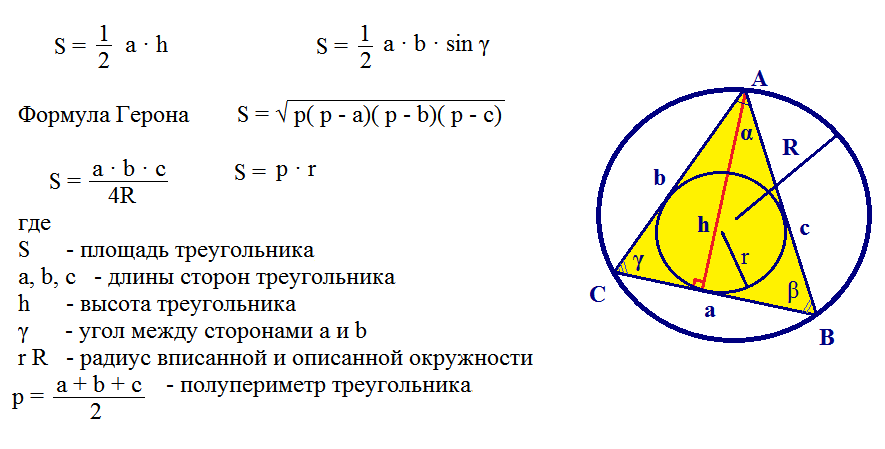
É difícil resolver problemas semelhantes, mas podem ser superados se você conhecer todas as fórmulas. Os alunos resolvem essas tarefas no 9º ano.

Área de um círculo inscrito em um trapézio retangular e isósceles: fórmula, exemplos de resolução de problemas

Por exemplo, um trapézio isósceles é inscrito com um círculo que está no ponto de contato divide um lado em segmentos m e n.

Para resolver este problema, você precisa usar as seguintes fórmulas:

Encontrar a área de um círculo inscrito em um trapézio retangular é realizado de acordo com a seguinte fórmula:

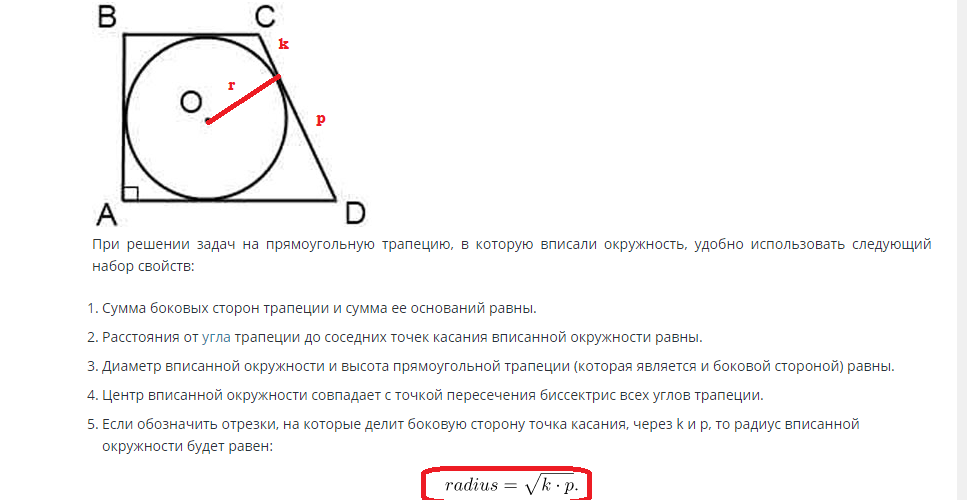
Se o lado é conhecido, então o raio pode ser encontrado através deste valor. A altura do lado do trapézio é igual ao diâmetro do círculo e o raio é metade do diâmetro. Assim, o raio é igual a R=d/2.

Exemplos de resolução de problemas:

Área de um círculo circunscrito a um trapézio retângulo e isósceles: fórmula, exemplos de resolução de problemas

Um trapézio pode ser inscrito em um círculo quando a soma dos ângulos opostos é 180°. Portanto, apenas um trapézio equilátero pode ser inscrito. O raio para calcular a área de um círculo descrito perto de um trapézio retangular ou isósceles é calculado usando as seguintes fórmulas:

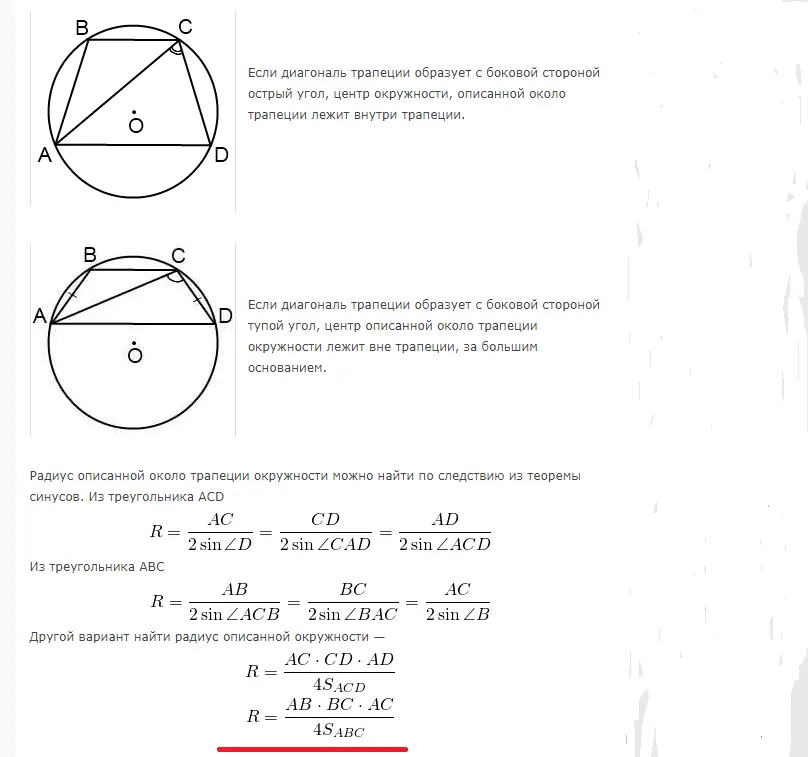
Exemplos de resolução de problemas:

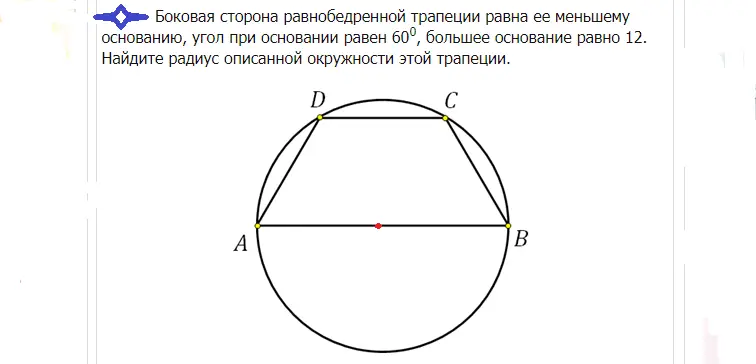
Solução: A base grande neste caso passa pelo centro, como um trapézio isósceles inscrito no círculo. O centro divide essa base exatamente ao meio. Se a base AB for igual a 12, então o raio R pode ser encontrado da seguinte forma: R=12/2=6.

Resposta: O raio é 6.

Em geometria, é importante conhecer fórmulas. Mas é impossível lembrar de todos eles, portanto, mesmo em muitos exames, é permitido usar um formulário especial. No entanto, é importante ser capaz de encontrar a fórmula certa para resolver este ou aquele problema. Pratique a resolução de vários problemas para encontrar o raio e a área de um círculo para poder substituir fórmulas corretamente e obter respostas precisas.

Vídeo: Matemática | Cálculo das áreas de um círculo e suas partes